[백준-1991(그래프)] 트리순회

시간 제한메모리 제한제출정답맞힌 사람정답 비율

2 초

128 MB

71432

46643

35868

67.185%

문제

 

이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.

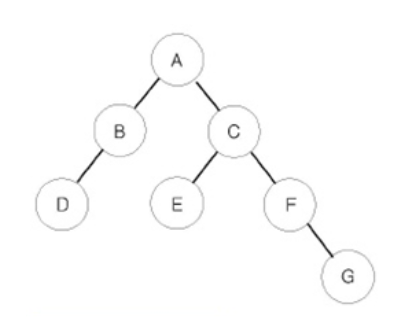
예를 들어 위와 같은 이진 트리가 입력되면,

• 전위 순회한 결과 : ABDCEFG // (루트) (왼쪽 자식) (오른쪽 자식)
• 중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
• 후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)

---

입력

첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파벳 대문자로 매겨지며, 항상 A가 루트 노드가 된다. 자식 노드가 없는 경우에는 .으로 표현한다.

 

---

출력

첫째 줄에 전위 순회, 둘째 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파벳을 공백 없이 출력하면 된다.

 

---

예제 입력 

7
A B C
B D .
C E F
E . .
F . G
D . .
G . .

예제 출력 

ABDCEFG
DBAECFG
DBEGFCA

---

문제 설명 요약

이 문제는 이진 트리의 구조가 주어졌을 때, 전위 순회(Preorder), 중위 순회(Inorder), **후위 순회(Postorder)**의 결과를 출력하는 전형적인 재귀 문제입니다.

• 전위 순회: 루트 → 왼쪽 → 오른쪽
• 중위 순회: 왼쪽 → 루트 → 오른쪽
• 후위 순회: 왼쪽 → 오른쪽 → 루트

트리는 문자(A~Z)로 주어지며, .는 자식 노드가 없음을 의미합니다.

 

입력 예시 및 시각화

7
A B C
B D .
C E F
E . .
F . G
D . .
G . .

이 입력은 다음과 같은 트리를 나타냅니다:

        A
       / \
      B   C
     /   / \
    D   E   F
               \
                G

---

순회 방식 요약

• 전위 순회 (Preorder): 루트 → 왼쪽 → 오른쪽 → 결과: ABDCEFG
• 중위 순회 (Inorder): 왼쪽 → 루트 → 오른쪽 → 결과: DBAECFG
• 후위 순회 (Postorder): 왼쪽 → 오른쪽 → 루트 → 결과: DBEGFCA

전체 코드 (딕셔너리, 재귀 구현)

# 표준 입력을 빠르게 받기 위해 sys 사용
import sys
input = sys.stdin.readline

# 트리 노드의 개수 입력받기
n = int(input())

# 트리 구조를 저장할 딕셔너리 선언
tree = {}

# 트리 구성 정보 입력받기
for _ in range(n):
    root, left, right = input().split()        # 루트, 왼쪽 자식, 오른쪽 자식 입력
    tree[root] = (left, right)                  # 딕셔너리에 저장: key=root, value=(left, right)

# 전위 순회 함수 정의 (Root → Left → Right)
def preorder(node):
    if node == '.':                             # 자식 노드가 없음을 의미하면 종료
        return
    print(node, end='')                         # 현재 노드 출력
    preorder(tree[node][0])                     # 왼쪽 자식 순회
    preorder(tree[node][1])                     # 오른쪽 자식 순회

# 중위 순회 함수 정의 (Left → Root → Right)
def inorder(node):
    if node == '.':
        return
    inorder(tree[node][0])                      # 왼쪽 자식 순회
    print(node, end='')                         # 현재 노드 출력
    inorder(tree[node][1])                      # 오른쪽 자식 순회

# 후위 순회 함수 정의 (Left → Right → Root)
def postorder(node):
    if node == '.':
        return
    postorder(tree[node][0])                    # 왼쪽 자식 순회
    postorder(tree[node][1])                    # 오른쪽 자식 순회
    print(node, end='')                         # 현재 노드 출력

# 순회 결과 출력 (문제 조건상 루트는 항상 'A')
preorder('A')
print()
inorder('A')
print()
postorder('A')
print()

 

Node 클래스 기반 코드 (객체지향 방식)

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

import sys
input = sys.stdin.readline

n = int(input())
nodes = {}

for _ in range(n):
    root, left, right = input().split()

    if root not in nodes:
        nodes[root] = Node(root)
    node = nodes[root]

    if left != '.':
        if left not in nodes:
            nodes[left] = Node(left)
        node.left = nodes[left]

    if right != '.':
        if right not in nodes:
            nodes[right] = Node(right)
        node.right = nodes[right]

def preorder(node):
    if node is None:
        return
    print(node.value, end='')
    preorder(node.left)
    preorder(node.right)

def inorder(node):
    if node is None:
        return
    inorder(node.left)
    print(node.value, end='')
    inorder(node.right)

def postorder(node):
    if node is None:
        return
    postorder(node.left)
    postorder(node.right)
    print(node.value, end='')

root = nodes['A']
preorder(root)
print()
inorder(root)
print()
postorder(root)
print()

---

 

---

정리

• 트리는 재귀적으로 순회하는 것이 핵심입니다.
• 문자 기반 트리는 딕셔너리 구조를 사용하면 간단하게 구현할 수 있습니다.
• 이 문제는 트리의 기초 순회를 연습하기 좋은 대표 문제입니다.
• 추후 트리 문제(예: 트리의 높이, 리프 개수, 특정 조건 탐색 등)로 확장 가능합니다.